از تبدیل خط هاف1 برای کشف خطوط استفاده می‌شود. برای اعمال این تبدیل نیاز است که ابتدا تصویر مورد نظر لبه‌یابی شود.

همانطور که می دانید، می‌توان خط را به وسیلهٔ دو پارامتر مشخص کرد. برای مثال:

a. در مختصات کارتزین پارمتر ها به صورت (m,b) هستند.

b. در مختصات قطبی پارامترها به صورت (r,ɵ) هستند.

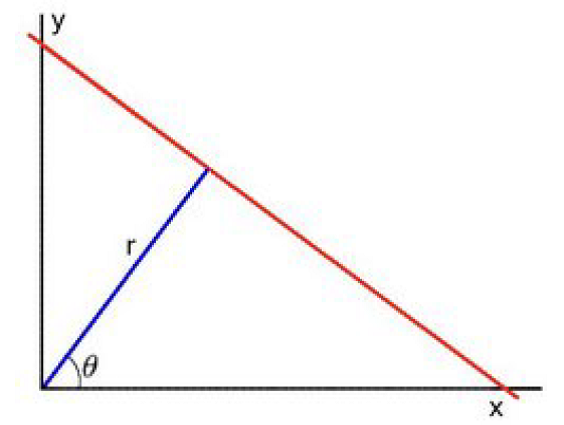یک خط و نحوه نمایش آن در مختصات کارتزین و قطبی

در تبدیل هاف از فرم قطبی استفاده می‌شود، بنابراین معادلهٔ خط را می‌توان به شکل زیر نوشت:

$$y = \left( - \frac{\cos\theta}{\sin\theta} \right)x + \left( \frac{r}{\sin\theta} \right)$$

که در آن $r = x\cos\theta + y\sin\theta$ است.

به طورکلی، به ازای هر نقطه به صورت $\left( x_{0},y_{0} \right)$ می‌توانیم خانوادهٔ خطوطی که از آن نقطه می‌گذرند را به صورت زیر تعریف کنیم:

$$r = x_{0}\cos\theta + y_{0}\sin\theta$$

هر جفت $\left( r_{\theta},\ \theta \right)$، نشان دهندهٔ یک خط است که از نقطهٔ$\left( x_{0},\ y_{0} \right)$ می گذرد.

اگر خانوادهٔ تمام خطوطی که از نقطهٔ $\left( x_{0},y_{0} \right)$ می‌گذرند را در صحفهٔ $\theta - r$ رسم کنیم، یک شکل سینوسی به وجود می‌آید. مثلاً به ازای $x_{0} = 8$ و $y_{0} = 6$ شکل زیر به وجود می‌آید:

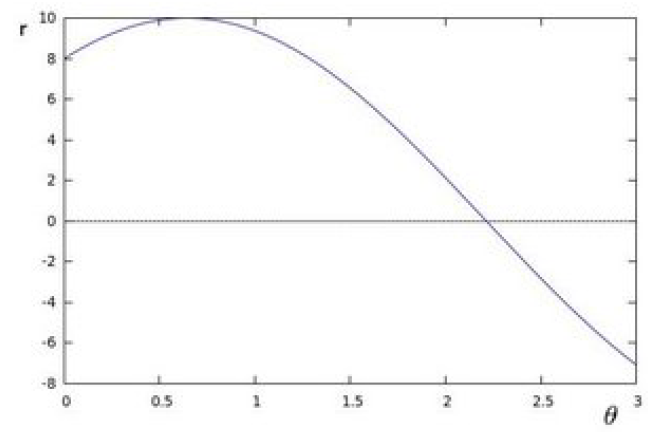جفت $\left( \mathbf{r}_{\mathbf{\theta}}\mathbf{,\ \theta} \right)$ تمام خطوطی که از نقطه $\left( \mathbf{8,\ 6} \right)$ می گذرند

می‌توان مشابه کار بالا را برای تمام نقاط موجود در یک تصویر انجام داد. اگر منحنی دو نقطهٔ مختلف در صفحهٔ $\theta - r$ هم دیگر را قطع کنند، به این معنی است که آن دو نقطه روی یک خط قرار دارند. مثلاً اگر به دنبال نقطهٔ مثال قبل، منحنی‌های نقاط $\left( 4,\ 9 \right)$ و $\left( 12,\ 3 \right)$ را بکشیم، نمودار حاصل به شکل زیر در می‌آید:

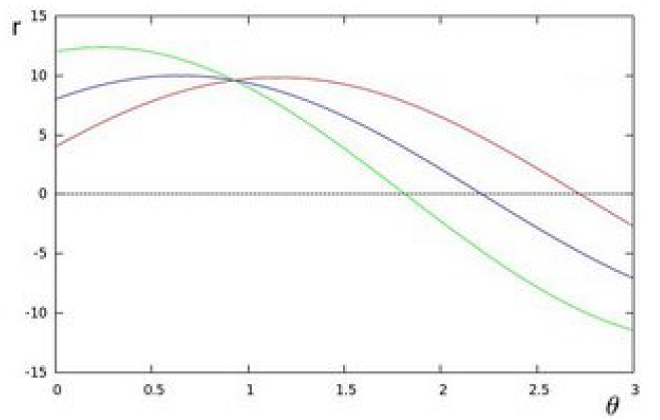رسم منحنی خطوطی که از سه نقطه $\left( \mathbf{8,\ 6} \right)$، $\left( \mathbf{4,9} \right)$ و $\left( \mathbf{12,\ 3} \right)$ می گذرند

در این نمودار، سه منحنی یکدیگر را در نقطهٔ $\left( 0.925,\ 9.6 \right)$ قطع کرده‌اند. این همان پارامترهای $\left( \theta,\ r \right)$ خطی است که نقاط $\left( 8,\ 6 \right)$، $\left( 4,9 \right)$ و $\left( 12,\ 3 \right)$ روی آن قرار گرفته‌اند.

به صورت کلی می‌توان یک خط را با به دست آوردن نقاط برخورد بین منحنی‌ها کشف کرد. هر چه تعداد بیشتری منحنی در یک برخورد وجود داشته باشد، به این معنی است که خطی که نشان دهندهٔ آن برخورد است، تعداد بیشتری نقطه دارد. به صورت کلی می‌توان با تعیین یک آستانه، حداقل تعداد مجاز برخوردهای مورد نیاز برای خط حساب کردن تعدادی نقطه را مشخص کرد. این همان کاری است که تبدیل هاف انجام می‌دهد. این تبدیل تعداد برخوردهای منحنی همه نقاط تصویر را به دست می‌آورد و اگر تعداد برخوردها بیشتر از آستانه بود، آن را به عنوان خط با پارامترهای $\left( \theta,r_{\theta} \right)$، در نظر می‌گیرد.

در اُ سی وی دو نوع تبدیل خط هاف پیاده سازی شده است:

تبدیل خط استاندارد هاف:

بسیار شبیه همان چیزی است که توضیح دادیم. به عنوان خروجی، برداری از جفت‌های $\left( \theta,r_{\theta} \right)$ را می‌دهد. این تبدیل در تابع HoughLines پیاده سازی شده است.

تبدیل خط احتمالی هاف:

این تبدیل بسیار بهینه‌تر از تبدیل خط استاندارد پیاده سازی شده است. به عنوان خروجی، نقاط انتهایی خطوط کشف شده را بر می‌گرداند $(x_{0},y_{0},x_{1},y_{1})$. این تبدیل در تابع HoughLinesP پیاده سازی شده است.

کد

#include "opencv2/highgui/highgui.hpp"
#include "opencv2/imgproc/imgproc.hpp"

#include <iostream>

using namespace cv;
using namespace std;

void help()
{
    cout << "\nThis program demonstrates line finding with the Hough transform.\n"
            "Usage:\n"
            "./houghlines <image_name>, Default is pic1.jpg\n" << endl;
}

int main(int argc, char** argv)
{

    Mat src = imread(argv[1], 0);
    if(src.empty())
    {
        help();
        cout << "can not open " << argv[1] << endl;
        return -1;
    }

    Mat dst, cdst;
    Canny(src, dst, 50, 200, 3);
    cvtColor(dst, cdst, CV_GRAY2BGR);

#if 0
    vector<Vec2f> lines;
    HoughLines(dst, lines, 1, CV_PI/180, 100, 0, 0 );

    for( size_t i = 0; i < lines.size(); i++ )
    {
        float rho = lines[i][0], theta = lines[i][1];
        Point pt1, pt2;
        double a = cos(theta), b = sin(theta);
        double x0 = a*rho, y0 = b*rho;
        pt1.x = cvRound(x0 + 1000*(-b));
        pt1.y = cvRound(y0 + 1000*(a));
        pt2.x = cvRound(x0 - 1000*(-b));
        pt2.y = cvRound(y0 - 1000*(a));
        line( cdst, pt1, pt2, Scalar(0,0,255), 3, CV_AA);
    }
#else
    vector<Vec4i> lines;
    HoughLinesP(dst, lines, 1, CV_PI/180, 50, 50, 10 );
    for( size_t i = 0; i < lines.size(); i++ )
    {
        Vec4i l = lines[i];
        line( cdst, Point(l[0], l[1]), Point(l[2], l[3]), Scalar(0,0,255), 3, CV_AA);
    }
#endif
    imshow("source", src);
    imshow("detected lines", cdst);

    waitKey();

    return 0;
}

توضیح

در خط 28 با استفاده از لبه‌یاب کَنی، لبه‌های عکس را پیدا می‌کنیم.

حالا می‌توانیم تبدیل خط هاف را اعمال کنیم. هر دو تابع اُ سی وی که برای این کار هستند را توضیح می‌دهیم:

تبدیل خط استاندارد هاف:

ابتدا در خط 33 تبدیل خط استاندارد را با استفاده از تابع HoughLines حساب می‌کنیم. این تابع 7 آرگومان دارد که به شرح زیر هستند:

1. dst: تصویر ورودی (که در حقیقت همان خروجی لبه‌یاب) است. این تصویر باید نوع سیاه و سفید باشد (اگر چه در حقیقت یک عکس باینری است).

2. lines: برداری که پارامترهای $(r,\ \theta)$ خطوط کشف شده در آن قرار می‌گیرند.

3. rho: وضوح پارامتر r بر حسب تعداد پیکسل‌ها است. در این جا از 1 پیکسل استفاده می‌کنیم.

4. theta: وضوح پارامتر $\theta$ بر حسب رادیان است. در اینجا از 1 درجه استفاده می‌کنیم (که یعنی CV_PI/180).

5. threshold: حداقل تعداد برخوردها برای در نظر گرفتن به عنوان خط است.

6. srn و stn: به صورت پیش‌فرض صفر هستند.

سپس در خطوط 35 تا 46 نتیجه را با کشیدن تمام خط‌های کشف شده، نشان می‌دهیم.

تبدیل خط احتمالی هاف:

ابتدا در خط 49 تبدیل خط احتمالی را با استفاده از تابع HoughLinesP حساب می‌کنیم. این تابع 7 آرگومان دارد که به شرح زیر هستند:

1. dst: تصویر ورودی (که در حقیقت همان خروجی لبه‌یاب) است. این تصویر باید از نوع سیاه و سفید باشد (اگر چه در حقیقت یک عکس باینری است).

2. lines: برداری که پارامترهای $(x_{\text{start}},\ y_{\text{start}},\ x_{\text{end}},\ y_{\text{end}})$ خطوط کشف شده در آن قرار می گیرند.

3. rho: وضوح پارامتر r بر حسب تعداد پیکسل‌ها است. در این جا از 1 پیکسل استفاده می‌کنیم.

4. theta: وضوح پارامتر $\theta$ بر حسب رادیان است. در اینجا از 1 درجه استفاده می‌کنیم (که یعنی CV_PI/180).

5. threshold: حداقل تعداد برخوردها برای در نظر گرفتن به عنوان خط است.

6. minLineLenght: حداقل تعداد نقطه‌هایی که می‌توانند یک خط را تشکیل دهند. خطوطی که کمتر از این تعداد نقطه دارند رد می‌شوند.

7. maxLineGap: حداکثر فضای خالی بین دو نقطه که روی یک خط قرار دارند.

سپس در خطوط 50 تا 54 نتیجه را با کشیدن تمام خط‌های کشف شده، نشان می‌دهیم.

خروجی

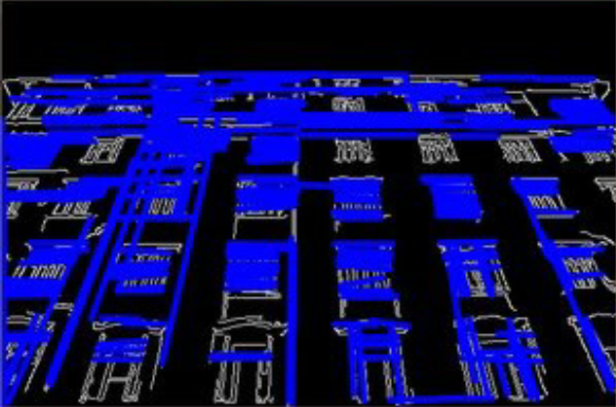تصویر ورودی	نتیجه اعمال تبدیل خط احتمالی هاف با آستانه 20