فصل سوم - حوزهٔ زمان

تبدیل فوریهٔ گسسته

تبدیل فوریه تصویر را به مؤلفه‌های سینوسی و کسینوسی آن تبدیل می‌کند. به عبارت دیگر، تصویر را از دامنهٔ مکانی1 به دامنهٔ زمانی یا فرکانسی2 می‌برد. اصل قضیه این است که هر تابع را می‌توان به صورت جمع تعداد بینهایت سینوس و کسینوس درآورد و تبدیل فوریه راهی برای انجام این کار است. به صورت ریاضی وار، تبدیل فوریهٔ دو بعدی برای یک تصویر به صورت زیر است:

$$F\left( k,l \right) = \ \sum_{i = 0}^{N - 1}{\sum_{j = 0}^{N - 1}{f\left( i,j \right)\ e^{- i2\pi\left( \frac{\text{ki}}{N} + \frac{\text{lj}}{N} \right)}}}$$

$$e^{\text{ix}} = cosx + isinx$$

در این معادله f مقدار تصویر در دامنهٔ مکانی و F هم مقدار تصویر در دامنهٔ زمانی است. نتیجهٔ این تبدیل اعداد مختلط است. می‌توانیم نتیجه را به صورت یک ماتریس از قسمت حقیقی3 و یک ماتریس از قسمت مجازی4 این اعداد و یا به صورت دامنه5 و فاز6 اعداد مختلط نشان دهیم. در اکثر الگوریتم‌های پردازش تصویر بیشتر با دامنه سروکار داریم؛ چون فاز یک تصویر اطلاعات اصلی آن تصویر را نگه داری می‌کند و هر گونه تغییر در مقادیر آن ممکن است باعث نابودی آن تصویر شود. ولی تغییر دامنه موجب تغییر در کیفیت تصویر می‌شود.

در زیر دامنه و فاز تصویر سمت چپ نشان داده شده است:


تصویر فاز	تصویر دامنه لگاریتمی	تصویر اصلی

برای بازسازی کامل یک تصویر از تبدیل فوریهٔ آن، هم به فاز و هم به دامنه آن تصویر نیاز است. در زیر می بینیدکه نتیجه بازسازی تصویر بالا فقط با استفاده از دامنه یا فاز آن به چه صورتی در می‌آید:


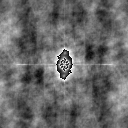فقط فاز	فقط دامنه

برای بازسازی یک تصویر فقط با استفاده از فاز آن باید مقدار دامنه را یک قرار دهیم و سپس عمل بازسازی را انجام دهیم. همچنین برای بازسازی یک تصویر فقط با استفاده از دامنه آن باید مقدار فاز را صفر قرار دهیم و سپس عمل بازسازی را انجام دهیم.

کد

#include "opencv2/core/core.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/highgui/highgui.hpp"

#include <iostream>

using namespace cv;

// Rearrange the quadrants of a Fourier image so that the origin is 
// at the image center
void shiftDFT(Mat &fImage )
{
    Mat tmp, q0, q1, q2, q3;

    // first crop the image, if it has an odd number of rows or columns

    fImage = fImage(Rect(0, 0, fImage.cols & -2, fImage.rows & -2));

    int cx = fImage.cols / 2;
    int cy = fImage.rows / 2;

    // rearrange the quadrants of Fourier image
    // so that the origin is at the image center

    q0 = fImage(Rect(0, 0, cx, cy));
    q1 = fImage(Rect(cx, 0, cx, cy));
    q2 = fImage(Rect(0, cy, cx, cy));
    q3 = fImage(Rect(cx, cy, cx, cy));

    q0.copyTo(tmp);
    q3.copyTo(q0);
    tmp.copyTo(q3);

    q1.copyTo(tmp);
    q2.copyTo(q1);
    tmp.copyTo(q2);
}

int main()
{
    // Load an image
    Mat I1 = imread("PICTURES/1.jpg", CV_LOAD_IMAGE_GRAYSCALE);
    Mat I2 = imread("PICTURES/2.jpg", CV_LOAD_IMAGE_GRAYSCALE);

    Mat fI1;
    Mat fI2;
    I1.convertTo(fI1, CV_32F);
    I2.convertTo(fI2, CV_32F);

    //expand input image to optimal size
    int m = getOptimalDFTSize( I1.rows );
    int n = getOptimalDFTSize( I1.cols );

    Mat padded1, padded2;

    // on the border add zero values
    copyMakeBorder(fI1, padded1, 0, m - I1.rows, 0, n - I1.cols, BORDER_CONSTANT, Scalar::all(0));
    copyMakeBorder(fI2, padded2, 0, m - I2.rows, 0, n - I2.cols, BORDER_CONSTANT, Scalar::all(0));

    //Perform DFT
    Mat fourierTransform1;
    Mat fourierTransform2;
    Mat planes1[2], planes2[2];

    dft(fI1, fourierTransform1, DFT_SCALE|DFT_COMPLEX_OUTPUT);
    dft(fI2, fourierTransform2, DFT_SCALE|DFT_COMPLEX_OUTPUT);

    // rearrange the quadrants of Fourier image
    shiftDFT(fourierTransform1);
    shiftDFT(fourierTransform2);

    split(fourierTransform1, planes1);// planes1[0] = Re(DFT(I1)), planes1[1] = Im(DFT(I1))
    split(fourierTransform2, planes2);// planes2[0] = Re(DFT(I2)), planes2[1] = Im(DFT(I2))

    Mat ph1, mag1;
    cartToPolar(planes1[0], planes1[1], mag1, ph1);

    Mat ph2, mag2;
    cartToPolar(planes2[0], planes2[1], mag2, ph2);

    /// if we want to show only the magnitude of the images:
    // ph1 = Mat::zeros(planes1[0].rows, planes1[0].cols, CV_32FC1);
    // ph2 = Mat::zeros(planes2[0].rows, planes2[0].cols, CV_32FC1);

    /// if we want to show only the phase of the images:
    // mag1 = Mat::ones(planes1[0].rows, planes1[0].cols, CV_32FC1);
    // mag2 = Mat::ones(planes2[0].rows, planes2[0].cols, CV_32FC1);

    polarToCart(mag2, ph1, planes1[0], planes1[1]);
    polarToCart(mag1, ph2, planes2[0], planes2[1]);

    merge(planes1, 2, fourierTransform1);
    merge(planes2, 2, fourierTransform2);

    // rearrange the quadrants of Fourier image
    shiftDFT(fourierTransform1);
    shiftDFT(fourierTransform2);

    //Perform IDFT
    Mat inverseTransform1, inverseTransform2;

    dft(fourierTransform1, inverseTransform1, DFT_INVERSE|DFT_REAL_OUTPUT);
    dft(fourierTransform2, inverseTransform2, DFT_INVERSE|DFT_REAL_OUTPUT);

    imshow("original image 1", I1);
    imshow("original image 2", I2);

    cv::Mat out1, out2;
    inverseTransform1.convertTo(out1, CV_8U);
    inverseTransform2.convertTo(out2, CV_8U);

    imshow("result image 1", out1);
    imshow("result image 2", out2);

    waitKey(0);
}

توضیح

ابتدا در خطوط 42 و 43 دو تصویر را از روی دیسک به صورت سیاه و سفید می‌خوانیم. بهتر است که ابعاد هر دو تصویر یکسان باشد؛ البته اگر هم اندازه نباشند هم در ادامه اندازه تصویر دوم هم اندازه تصویر اول می‌کنیم. می‌خواهیم در ادامه فاز و دامنه این دو تصویر را حساب کنیم و نمایش دهیم.

در خطوط 47 و 48، نوع عکس را از 8 بیتی صحیح به 32 بیتی اعشاری تبدیل می‌کنیم.

در خطوط 51 و 52 اندازه بهینه تصاویر برای انجام تبدیل فوریه را حساب می‌کنیم. برای اینکه عملیات تبدیل فوریه گسسته به صورت بهینه انجام شود، ابعاد تصویر مورد نظر بهتر است عددی باشد که بتوان آن را به صورت ضرب توان‌های سه عدد 2، 3 و 5 نوشت. می‌توان کوچکترین عدد بزرگتر از بُعد فعلی که همچین شرایطی داشته باشد را با استفاده از تابع getOptimalDFTSize به دست آورد. در اینجا ابتدا در خط 51 اندازه بهینه برای تعداد سطرها را به دست می‌آوریم و سپس اندازه بهینه برای تعداد ستون‌ها را حساب می‌کنیم. البته لازم به ذکر است که تابع dft می‌تواند با تصویر با هر ابعادی کار کند و این کارها فقط برای بهبود سرعت این تابع است.

در خطوط 54 تا 58 ابعاد تصاویر ورودی را افزایش می‌دهیم تا مطابق با ابعاد بهینه شوند. مثلاً برای افزایش ابعاد تصویر ورودی اول به صورت زیر از تابع copyMakeBorder استفاده می‌کنیم:

copyMakeBorder(fI1, padded1, 0, m - I1.rows, 0, n - I1.cols, BORDER_CONSTANT, Scalar::all(0));

این تابع برای افزایش ابعاد تصویر ورودی یک قاب با اندازه مشخص شده به اطراف تصویر اضافه می‌کند. در اینجا fI1 تصویر ورودی و padded1 نام ماتریسی است که خروجی در آن قرار می‌گیرد. بعد از آن چهار عدد آمده که عدد اول مشخص کننده اندازه قاب بالایی، عدد دوم اندازه قاب پایینی، عدد سوم اندازه قاب سمت راست و عدد چهارم اندازه قاب سمت چپ است. دو آرگومان آخر به معنی این است که می‌خواهیم رنگ قاب یکنواخت و سیاه باشد.

در خطوط 65 و 66 با استفاده از تابع dft، تبدیل فوریه گسسته دو تصویر ورودی (که به ابعاد بهینه در آمده‌اند) را حساب می‌کنیم. در این تابع از دو پرچم استفاده کرده‌ایم. DFT_SCALES مشخص می‌کند که خروجی بر تعداد عناصر ماتریس تقسیم شود. DFT_COMPLEX_OUTPUT هم مشخص می‌کند که خروجی به صورت عدد مختلط در فضای کارتزین باشد.

در خطوط 69 و 70 مرکز تبدیل فوریه را از چهار گوشه به مرکز ماتریس منتقل می‌کنیم. این کار را با صدا زدن تابع shiftDFT انجام می‌دهیم.

ماتریس‌های fourierTransform1 و fourierTransform2 دو کاناله هستند. در کانال اول قسمت حقیقی تبدیل فوریه و در کانال دوم قسمت مجازی تبدیل فوریه قرار دارد. برای اینکه راحت‌تر به این دو مؤلفه دسترسی داشته باشیم، در خطوط 72 و 73، با استفاده از تابع split کانال‌های ماتریس‌های fourierTransform1 و fourierTransform2 را جدا می‌کنیم و در آرایه planes1 و planes2 قرار می‌دهیم. توجه کنید که در اینجا داده‌های ماتریس‌ها کپی نمی‌شوند و فقط اشاره گری به آنها بر گردانده می‌شود.

در خطوط 76 و 79 با استفاده از تابع cartToPolar مختصه‌های planes1 و planes2 را از فضای کارتزین به فضای قطبی می‌بریم و نتیجه را در mag1،ph1 و mag2،ph2 ذخیره می‌کنیم. حالا به فاز و دامنه تصاویر دسترسی داریم. می‌توانیم آن‌ها را نمایش دهیم و یا تغییر دهیم و یا هر کاری می‌خواهیم با آنها انجام دهیم. در ادامه می‌خواهیم برای بازسازی تصویر اول از دامنه تصویر دوم و برای تصویر دوم از دامنه تصویر اول استفاده کنیم.

اگر می‌خواهید تصاویر نهایی را فقط با استفاده از دامنه بازسازی کنید، لازم است که فاز هر دو تصویر را صفر کنید. برای اینکار خطوط 82 و 83 را باید از حالت توضیح خارج کنید. همچنین اگر می‌خواهید تصاویر نهایی را فقط با استفاده از فاز بازسازی کنید، لازم است که دامنه هر دو تصویر را یک کنید. برای اینکار خطوط 86 و 87 را باید از حالت توضیح خارج کنید.

در خطوط 89 و 90 با استفاده از تابع polarToCart مؤلفه‌های فوریه تصاویر را از مختصات قطبی به مختصات کارتزین می‌بریم. در اینجا ماتریس‌های mag1،ph1 و mag2،ph2 مؤلفه‌های مختصات قطبی هستند. نتیجه در planes1 و planes2 ذخیره می‌شود. توجه کنید که در خط 89 برای بازسازی تصویر اول از دامنه تصویر دوم استفاده کرده‌ایم، همچنین در خط 90 برای بازسازی تصویر دوم از دامنه تصویر اول استفاده کرده‌ایم.

در خط 92 با استفاده از تابع merge دو ماتریس موجود در آرایه planes1 را به یک ماتریس دو کاناله تبدیل می‌کنیم و در ماتریس fourierTransform1 قرار می‌دهیم. همین کار را در خط 93 برای planes2 انجام می‌دهیم.

در خطوط 96 و 97 مجدداً مرکز ماتریس تبدیل فوریه را به چهار گوشه منتقل می‌کنیم.

در خطوط 102 و 103 تبدیل معکوس فوریه را انجام می‌دهیم. مثلاً در خط 102 به صورت زیر عمل می‌کنیم:

dft(fourierTransform1, inverseTransform1, DFT_INVERSE|DFT_REAL_OUTPUT);

در اینجا fourierTransform1 ماتریس دو کاناله ای است که در آن تبدیل فوریه به فرم اعداد مختلط در فضای کارتزین قرار دارد. خروجی که به صورت یک ماتریس تک کاناله از اعداد حقیقی است، در ماتریس inverseTransform1 قرار می‌گیرد. پرچم DFT_INVERSE بدین معناست که می‌خواهیم تبدیل معکوس فوریه انجام دهیم و DFT_REAL_OUTPUT به این معنی است که می‌خواهیم خروجی به صورت اعداد حقیقی باشد.

در خطوط 109 و 110 ماتریس‌هایی که از تبدیل فوریه معکوس به دست آمده بوداند را به نوعِ 8 بیتی تبدیل می‌کنیم و سرانجام در خطوط 112 و 113 خروجی نهایی را نشان می‌دهیم.

خروجی


تصویر ورودی اول	تصویر ورودی دوم


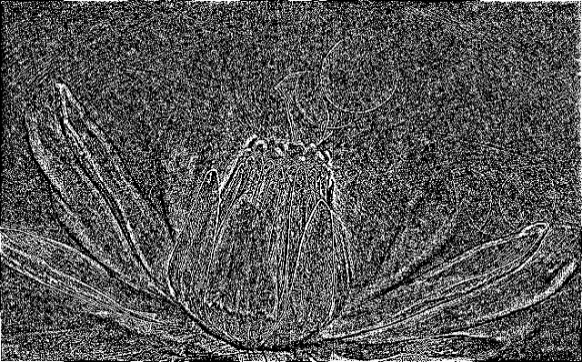
بازسازی تصویر اول فقط با استفاده از فاز آن	بازسازی تصویر دوم فقط با استفاده از فاز آن


بازسازی تصویر اول فقط با استفاده از دامنه آن	بازسازی تصویر دوم فقط با استفاده از دامنه آن


بازسازی تصویر اول با استفاده از فاز خودش و دامنه تصویر دوم	بازسازی تصویر دوم با استفاده از فاز خودش و دامنه تصویر اول

Domain Spatial ↩
Frequency Domain ↩
Real ↩
Imaginary ↩
Magnitude ↩
Phase ↩