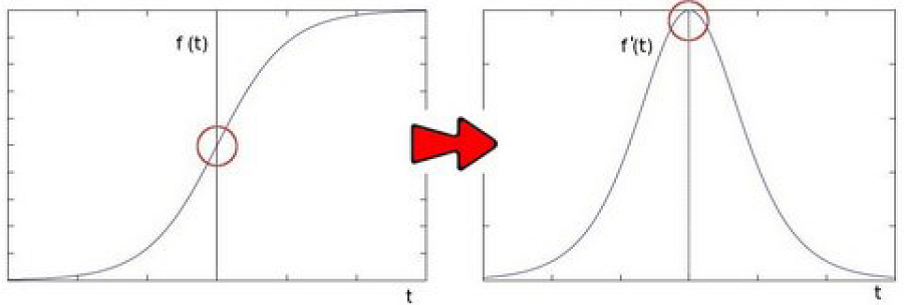
در بخش قبل با نحوهٔ استفاده از عملگر سابل آشنا شدید. این عملگر بر مبنای تغییرات روشنایی پیکسل‌های عکس بود. با گرفتن مشتق اول از تابع روشنایی دیدیم که می‌توان لبه را به عنوان یک بیشینه در نظر گرفت. مثلاً مشتق اول یک تابع می‌تواند به شکل زیر باشد:

یک تابع و مشتق آن

و وقتی مشتق دوم گرفته شود به شکل زیر خواهد بود:

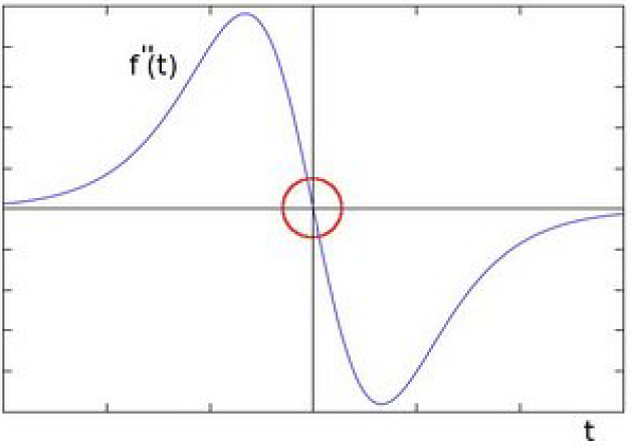
مشتق دوم تابع بالا

همانطور که می‌بینید، محل مورد نظر در مشتق دوم برابر صفر است! بنابراین می‌توان از این قضیه برای پیدا کردن لبه‌های یک تصویر استفاده کرد. توجه کنید که نقطه‌های صفر فقط در لبه‌ها رخ نمی‌دهند (می‌توانند در نقطه‌های بی معنی نیز رخ دهند)؛ البته می‌توان این مشکل را تا حدودی با فیلتر کردن نقاط برطرف کرد. در ادامه با عملگر لاپلاس آشنا می‌شویم.

عملگر لاپلاس:

از توضیحات بالا بر می‌آید که می‌توان از مشتق دوم برای پیدا کردن لبه‌ها استفاده کرد و از آنجایی که تصاویر دوبُعدی هستند، باید از هر دو بُعد مشتق بگیریم. اینجاست که عملگر لاپلاس به کار می‌آید و به‌صورت زیر تعریف می‌شود:

$$Laplace\left( f \right) = \ \frac{\partial^{2}f}{\partial x^{2}} + \frac{\partial^{2}f}{\partial y^{2}}$$

در اُ سی وی تابعی به نام Laplacian وجود دارد که معادلهٔ بالا را پیاده سازی کرده است. در واقع از آنجایی که لاپلاس از گرادیان‌های تصویر استفاده می‌کند، این تابع به صورت داخلی از عملگر سابل برای محاسباتش استفاده می‌کند.

کد

#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/highgui/highgui.hpp"
#include <stdlib.h>
#include <stdio.h>

using namespace cv;

/** @function main */
int main( int argc, char** argv )
{
    Mat src, src_gray, dst;
    int kernel_size = 3;
    int scale = 1;
    int delta = 0;
    int ddepth = CV_16S;
    char* window_name = "Laplace Demo";

    int c;

    /// Load an image
    src = imread( argv[1] );

    if( !src.data )
    { return -1; }

    /// Remove noise by blurring with a Gaussian filter
    GaussianBlur( src, src, Size(3,3), 0, 0, BORDER_DEFAULT );

    /// Convert the image to grayscale
    cvtColor( src, src_gray, CV_RGB2GRAY );

    /// Create window
    namedWindow( window_name, CV_WINDOW_AUTOSIZE );

    /// Apply Laplace function
    Mat abs_dst;

    Laplacian( src_gray, dst, ddepth, kernel_size, scale, delta, BORDER_DEFAULT );
    convertScaleAbs( dst, abs_dst );

    /// Show what you got
    imshow( window_name, abs_dst );

    waitKey(0);

    return 0;
}

توضیح

در خط 27 به منظور کاهش نویز از فیلتر هموار ساز گوسی استفاده می‌کنیم.

در خط 38 عملگر لاپلاس را با استفاده از تابع Laplacian به تصویر ورودی اعمال می‌کنیم. این تابع 7 آرگومان به شرح زیر دارد:

1. src_gray: تصویر ورودی (که در این مورد سیاه و سفید است. می‌تواند رنگی نیز باشد).
2. dst: تصویر خروجی
3. ddepth: عمق تصویر خروجی است. از آنجا که در اینجا تصویر ورودی از نوع CV_8U است، برای جلوگیری از سرریز، عمق تصویر خروجی را CV_16S می‌گذاریم.
4. kernel_size: اندازهٔ کرنل عملگر سابل که داخل تابع Laplacian استفاده می‌شود. در اینجا از اندازهٔ 3 استفاده می‌کنیم.
5. scale، delta و BORDER_DEFAULT: این‌ها را به صورت پیش‌فرض رها می‌کنیم.

در خط 39 خروجی تابع Laplacian را به نوع CV_8U تبدیل می‌کنیم.

خروجی

تصویر ورودی	تصویر خروجی

درخت‌ها و نیمرخ گاو خوب در آمده‌اند؛ البته ناحیه‌هایی که دارای روشنایی یکسان هستند، مثل اطراف سر گاو، خیلی خوب نشده‌اند. همانطور که می‌بینید به دلیل کنتراست زیاد ناحیه سقف خانه پشت گاو، لبه‌ها خیلی واضح مشخص شده‌اند.