فصل دوم - حوزهٔ مکان
عملگر سابل
پیدا کردن مشتقهای یک تصویر در کاربردهایی مثل یافتن لبههای موجود در تصویر مفید است.
 |
|---|
| قسمت مشخص شده با دایره قرمز یک لبه است |
به راحتی میتوان دید که در یک لبه روشنایی پیکسلها به شدت تغییر میکند. یکی از روشهای توصیف تغییرات، مشتقها هستند. یک تغییر زیاد در شیب، نماینگر یک تغییر قابل توجه در روشنایی تصویر است.
برای اینکه قضیه واضحتر شود، فرض کنید یک تصویر تک بعدی به صورت زیر داریم. محلی که با دایره قرمز مشخص شده است یک لبه است. این نقطه جایی است که تغییر قابل توجهی در شدت روشنایی دارد.
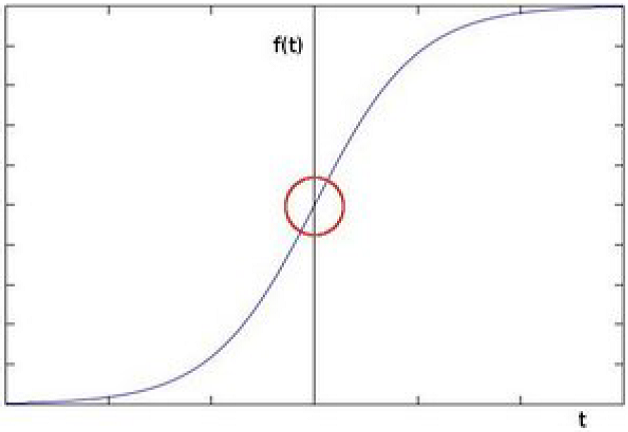 |
|---|
| یک تصویر یک بعدی - ناحیه مشخص شده با دایره قرمز یک لبه است |
میتوان محل لبهها را به راحتی با گرفتن مشتق اول پیدا کرد (در اینجا به شکل یک نقطهٔ بیشینه در آمده است).
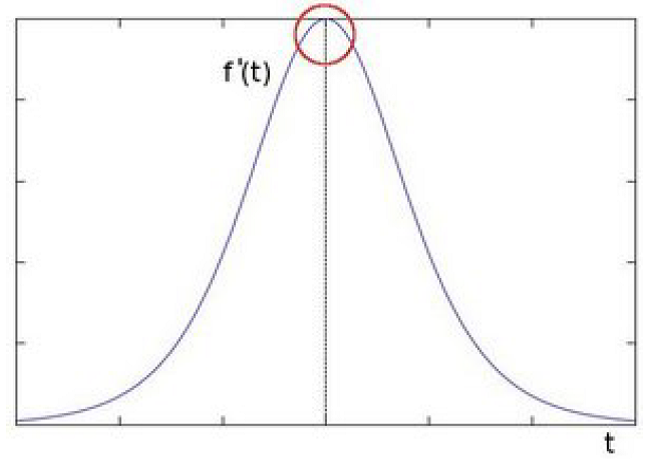 |
|---|
| مشتق تصویر تک بعدی قبل |
از توضیحات بالا نتیجه میگیریم که یک راه برای پیدا کردن لبههای تصویر این است که به دنبال پیکسلهایی بگردیم که گرادیانشان بیشتر از گرادیان همسایههایشان (یا به طور کلی بیشتر از یک آستانه) است. در ادامه نحوه به دست آوردن گرداین تصویر را به کمک عملگر سابل بررسی میکنیم.
عملگر سابل:
عملگر سابل1 یک عملگر دیفرانسیلیِ گسسته است. این عملگر به طور تقریبی گرادیان تابع روشنایی عکس را حساب میکند.
عملگر سابل، دو عمل هموار سازی گوسی و دیفرانسیل گیری را با هم ترکیب میکند.
با فرض اینکه عکس مورد نظر I باشد، روند کار این عملگر به صورت زیر است:
دو مشتق زیر را حساب میکند:
i. مشتق افقی: از طریق کانوالو I با کرنلی با اندازهٔ فرد به دست میآید. مثلاً برای کرنلی با اندازهٔ 3، $G_{x}$ (مشتق در راستای افقی) به شکل زیر به دست میآید:
$$ G_{x} = \begin{bmatrix} - 1 & 0 & + 1 \\ - 2 & 0 & + 2 \\ - 1 & 0 & + 1 \end{bmatrix}*I $$
ii. مشتق عمودی: از طریق کانوالو I با کرنلی با اندازهٔ فرد به دست میآید. مثلاً برای کرنلی با اندازهٔ 3، $G_{y}$ (مشتق در راستای عمودی) به شکل زیر به دست میآید:
$$ G_{y} = \begin{bmatrix} - 1 & - 2 & - 1 \\ 0 & 0 & 0 \\ + 1 & + 2 & + 1 \end{bmatrix}*I $$
برای به دست آوردن گرادیان پیکسلهای تصویر باید $G_{x}$ و $G_{y}$ را به شکل زیر با هم ترکیب کرد:
$$G = \sqrt{G_{x}^{2} + G_{y}^{2}}$$البته بعضی اوقات از معادله سادهتر زیر هم استفاده میشود:
$$G = \left| G_{x} \right| + |G_{y}|$$
نکته: وقتی اندازهٔ کرنل 3 است، کرنل سابلی که در قسمت قبل نشان داده شد میتواند به صورت قابل توجه ای نتایج نادرست تولید کند (به هر حال سابل فقط یک تقریب برای مشتقات است). در اُ سی وی برای حل این مشکل تابع Scharr ارائه شده که به اندازهٔ سابل سریع است و البته در عین حال دقتی بسیار بیشتر از آن دارد. تابع Scharr از کرنلهای زیر استفاده میکند:
$$ \mathbf{G}_{\mathbf{x}}\mathbf{=}\begin{bmatrix} \mathbf{- 3} & \mathbf{0} & \mathbf{+ 3} \\ \mathbf{- 10} & \mathbf{0} & \mathbf{+ 10} \\ \mathbf{- 3} & \mathbf{0} & \mathbf{+ 3} \end{bmatrix} $$
$$ \mathbf{G}_{\mathbf{y}}\mathbf{=}\begin{bmatrix} \mathbf{- 3} & \mathbf{- 10} & \mathbf{- 3} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{+ 3} & \mathbf{+ 10} & \mathbf{+ 3} \end{bmatrix} $$
کد
#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/highgui/highgui.hpp"
#include <stdlib.h>
#include <stdio.h>
using namespace cv;
/** @function main */
int main( int argc, char** argv )
{
Mat src, src_gray;
Mat grad;
char* window_name = "Sobel Demo - Simple Edge Detector";
int scale = 1;
int delta = 0;
int ddepth = CV_16S;
int c;
/// Load an image
src = imread( argv[1] );
if( !src.data )
{ return -1; }
GaussianBlur( src, src, Size(3,3), 0, 0, BORDER_DEFAULT );
/// Convert it to gray
cvtColor( src, src_gray, CV_RGB2GRAY );
/// Create window
namedWindow( window_name, CV_WINDOW_AUTOSIZE );
/// Generate grad_x and grad_y
Mat grad_x, grad_y;
Mat abs_grad_x, abs_grad_y;
/// Gradient X
//Scharr( src_gray, grad_x, ddepth, 1, 0, scale, delta, BORDER_DEFAULT );
Sobel( src_gray, grad_x, ddepth, 1, 0, 3, scale, delta, BORDER_DEFAULT );
convertScaleAbs( grad_x, abs_grad_x );
/// Gradient Y
//Scharr( src_gray, grad_y, ddepth, 0, 1, scale, delta, BORDER_DEFAULT );
Sobel( src_gray, grad_y, ddepth, 0, 1, 3, scale, delta, BORDER_DEFAULT );
convertScaleAbs( grad_y, abs_grad_y );
/// Total Gradient (approximate)
addWeighted( abs_grad_x, 0.5, abs_grad_y, 0.5, 0, grad );
imshow( window_name, grad );
waitKey(0);
return 0;
}
توضیح
در خط 27 برای کاهش نویز یک هموار سازی گوسی به تصویر ورودی اعمال میکنیم (با اندازه کرنل 3).
در خطوط 41 و 46 به ترتیب مشتقات در جهتهای x و y را حساب میکنیم. برای این کار از تابع Sobel استفاده میکنیم. این تابع 9 آرگومان به شرح زیر دارد:
- src_gray: تصویر ورودی است. در اینجا از نوع CV_8U است.
- grad_x/grad_y: تصویر خروجی
- ddepth: عمق تصویر خروجی است. برای جلوگیری از سرریز از CV_16S استفاده میکنیم.
- x_order: مرتبهٔ مشتق در جهت x است.
- y_order: مرتبهٔ مشتق در جهت y است.
- scale، delta و BORDER_DEFAULT: از مقادیر پیشفرض استفاده میکنیم.
توجه کنید که برای به دست آوردن گرادیان در جهت x باید $x_{\text{order}} = 1$ و $y_{\text{order}} = 0$ قرار دهیم. برعکس این کار را برای جهت y انجام می دهیم.
در خطوط 42 و 47، نتایج جزئی را به نوع CV_8U تبدیل میکنیم.
سرانجام در خط 50 برای تخمین گرادیان کلی، گردایان در جهتهای x و y را با هم جمع میکنیم (توجه کنید که این کار اصلاً یک محاسبه دقیق نیست!! ولی کار ما را راه میاندازد).
خروجی
 |
 |
|---|---|
| تصویر ورودی | تصویر خروجی |
Sobel ↩