فصل دوم - حوزهٔ مکان

هموار سازی تصویر

هموار سازی یا مات کردن، یک عمل سادهٔ پردازش تصویری است که بسیار مورد استفاده قرار می‌گیرد. دلایل زیادی برای هموار کردن یک تصویر وجود دارد. در این بخش از هموار کردن برای کاهش نویز استفاده می‌کنیم (با کاربردهای دیگرِ آن در بخش‌های دیگر آشنا خواهید شد).

به منظور هموار کردن تصویر باید از فیلترها استفاده کرد که عموماً از فیلترهای خطی استفاده می‌شود؛ در این فیلترها مقدار یک پیکسل خروجی (یعنی $g\left( i,j \right)$) به جمع وزن دار پیکسل‌های ورودی بستگی دارد (یعنی $f\left( i + k,j + l \right)$).

$$g\left( i,j \right) = \ \sum_{k,l}^{}{f\left( i + k,j + l \right)h(k,l)}$$

به $h(k,l)$ کرنل می گویند. کرنل همان ضرایب فیلتر است.

معادله بالا به ما نشان می‌دهد که فیلتر، یک پنجرهٔ لغزنده از ضرایب است که روی تصویر حرکت می‌کند. از آنجا که فیلترهای متنوع زیادی وجود دارند، اینجا فقط آنهایی که بیشتر مورد استفاده قرار می‌گیرند را توضیح می‌دهیم:

فیلتر جعبه‌ای نرمال شده1:

ساده‌ترین فیلتر موجود است که هر پیکسل خروجی، میانگین همسایه‌های آن است.
کرنل این فیلتر به صورت زیر است:

$$ K = \frac{1}{K_{width}.K_{height}}\begin{bmatrix} 1 & \cdots & 1 \\\\ \vdots & \ddots & \vdots \\\\ 1 & \cdots & 1 \end{bmatrix} $$

فیلتر گوسی2:

احتمالاً کاربردی‌ترین فیلتر (اما نه سریع‌ترین) است. فیلتر کردن به روش گوسی از کانوال هر نقطهٔ موجود در آرایه ورودی با یک کرنل گوسی و سپس جمع همهٔ آنها برای به دست آوردن خروجی، انجام می‌شود.
نمودار کرنل گوسی یک بعدی به صورت زیر است:

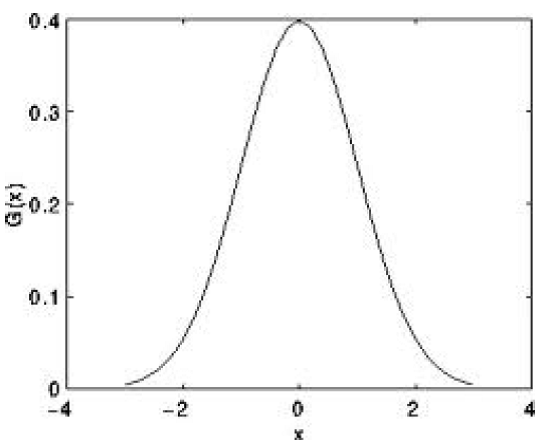
تابع توزیع گوسی

اگر فرض کنیم عکس یک بُعدی باشد، با توجه به شکل بالا پیکسلی که در مرکز قرار گرفته بزرگترین وزن را خواهد داشت. با افزایش فاصله از پیکسل مرکزی وزن‌ها نیز کمتر می‌شوند.


تابع توزیع گوسی

نکته: به یاد داشته باشید که گوسی دو بعدی به شکل زیر است:

$$G_{0}\left( x,y \right) = Ae^{\frac{- {(x - \mu_{x})}^{2}}{2\sigma_{x}^{2}}+\frac{- {(y - \mu_{y})}^{2}}{2\sigma_{y}^{2}}}$$

که $\mu$ نشان دهندهٔ میانگین و $\sigma$ نشان دهندهٔ انحراف معیار (به ازای متغییر های $x$ و $y$) است.

فیلتر میانه3:

فیلتر میانه گیر روی پیکسل‌های عکس عبور می‌کند و هر پیکسل را با میانهٔ پیکسل‌های همسایه‌اش جایگزین می‌کند.

فیلتر دوگانه4:

تا اینجا فیلترهایی معرفی کردیم که هدف اصلیشان هموار کردن تصویر ورودی بود. برخی اوقات فیلترها نه فقط نویزها را از بین می‌برند بلکه لبه‌ها را نیز از بین می‌برند. برای جلوگیری از مورد دوم (حداقل در برخی مواقع) می‌توان از فیلتر دوگانه استفاده کرد.

فیلتر دوگانه به روشی مشابه با فیلتر گوسی به هر کدام از پیکسل‌های همسایه، وزنی اختصاص می‌دهد. هر وزن از دو قسمت تشکیل شده است؛ قسمت اول همان وزنی است که در فیلتر گوسی وجود دارد. قسمت دوم هم اختلاف بین روشنایی پیکسل فعلی با همسایه‌هایش است. چون هدف این کتاب آموزش اُ سی وی است از ذکر جزئیات این فیلتر خودداری می‌کنیم.

کد

#include <iostream>
#include <vector>

#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/highgui/highgui.hpp"
#include "opencv2/features2d/features2d.hpp"

using namespace std;
using namespace cv;

/// Global Variables
int DELAY_CAPTION = 1500;
int DELAY_BLUR = 100;
int MAX_KERNEL_LENGTH = 31;

Mat src; Mat dst;
char window_name[] = "Smoothing Demo";

/// Function headers
int display_caption( const char* caption );
int display_dst( int delay );


/**
 * function main
 */
int main( void )
{
  namedWindow( window_name, WINDOW_AUTOSIZE );

  /// Load the source image
  src = imread( "D:/TRANSLATION/OpenCV Book for PGU/PICTURES/USED IN CODES/1.jpg", 1 );

  if( display_caption( "Original Image" ) != 0 ) { return 0; }

  dst = src.clone();
  if( display_dst( DELAY_CAPTION ) != 0 ) { return 0; }


  /// Applying Homogeneous blur
  if( display_caption( "Homogeneous Blur" ) != 0 ) { return 0; }

  for ( int i = 1; i < MAX_KERNEL_LENGTH; i = i + 2 )
      { blur( src, dst, Size( i, i ), Point(-1,-1) );
        if( display_dst( DELAY_BLUR ) != 0 ) { return 0; } }


  /// Applying Gaussian blur
  if( display_caption( "Gaussian Blur" ) != 0 ) { return 0; }

  for ( int i = 1; i < MAX_KERNEL_LENGTH; i = i + 2 )
      { GaussianBlur( src, dst, Size( i, i ), 0, 0 );
        if( display_dst( DELAY_BLUR ) != 0 ) { return 0; } }


  /// Applying Median blur
  if( display_caption( "Median Blur" ) != 0 ) { return 0; }

  for ( int i = 1; i < MAX_KERNEL_LENGTH; i = i + 2 )
      { medianBlur ( src, dst, i );
        if( display_dst( DELAY_BLUR ) != 0 ) { return 0; } }


  /// Applying Bilateral Filter
  if( display_caption( "Bilateral Blur" ) != 0 ) { return 0; }

  for ( int i = 1; i < MAX_KERNEL_LENGTH; i = i + 2 )
      { bilateralFilter ( src, dst, i, i*2, i/2 );
        if( display_dst( DELAY_BLUR ) != 0 ) { return 0; } }

  /// Wait until user press a key
  display_caption( "End: Press a key!" );

  waitKey(0);

  return 0;
}

/**
 * @function display_caption
 */
int display_caption( const char* caption )
{
  dst = Mat::zeros( src.size(), src.type() );
  putText( dst, caption,
           Point( src.cols/4, src.rows/2),
           FONT_HERSHEY_COMPLEX, 1, Scalar(255, 255, 255) );

  imshow( window_name, dst );
  int c = waitKey( DELAY_CAPTION );
  if( c >= 0 ) { return -1; }
  return 0;
}

/**
 * @function display_dst
 */
int display_dst( int delay )
{
  imshow( window_name, dst );
  int c = waitKey ( delay );
  if( c >= 0 ) { return -1; }
  return 0;
}

توضیح

در فصل قبل با خیلی از دستورهایی که در کد بالا استفاده شده‌اند، آشنا شدید؛ به همین دلیل فقط به توابع هموار سازی می‌پردازیم.

فیلتر جعبه‌ای نرمال شده (خط 44):

تابع blur چهار آرگومان دارد:

src: عکس منبع
dst: عکس مقصد
Size( w,h ): اندازهٔ کرنل مورد استفاده را مشخص می‌کند (عرض w و ارتفاع h).
Point( -1, -1 ): موقعیت نقطه لنگر5 نسبت به همسایه‌ها را مشخص می‌کند. اگر یک مقدارِ منفی باشد، مرکز کرنل به عنوان نقطهٔ مرجع در نظر گرفته می‌شود.

فیلتر گوسی (خط 52):

تابع GassuainBlur پنج آرگومان دارد:

src: عکس منبع
dst: عکس مقصد
Size( w, h): اندازهٔ کرنل مورد استفاده را مشخص می‌کند (یعنی همسایه‌های درگیر را مشخص می‌کند). w و h باید مثبت و فرد باشند، در غیر این صورت از $\sigma_{x}$ و $\sigma_{y}$ برای محاسبهٔ این اندازه‌ها استفاده می‌شود.
$\sigma_{x}$: انحراف معیار6 نسبت به x است. با قرار دادن مقدار صفر مشخص می‌کنیم که $\sigma_{x}$ باید از روی اندازهٔ کرنل محاسبه شود.
$\sigma_{y}$: انحراف معیار نسبت به y است. با قرار دادن مقدار صفر مشخص می‌کنیم که $\sigma_{y}$ باید از روی اندازهٔ کرنل محاسبه شود.

فیلتر میانه (خط 60):

تابع medianFilter سه آرگومان دارد:

src: عکس منبع
dst: عکس مقصد؛ باید همنوع src باشد.
i: اندازهٔ کرنل است (چون از کرنل مربعی استفاده می‌شود فقط یک پارامتر کافی است). باید فرد باشد.

فیلتر دوگانه (خط 68):

تابع bilateralFilter پنج آرگومان دارد:

src: تصویر منبع
dst: تصویر مقصد
d: قطر همسایگی هر پیکسل
$\sigma_{\text{color}}$: انحراف معیار در فضای رنگی.
$\sigma_{\text{space}}$: انحراف معیار در فضای مختصات (در مقیاس پیکسل).

خروجی

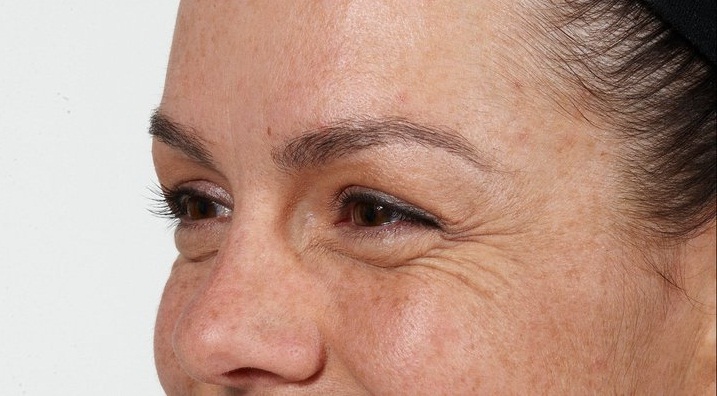
برنامه پس از اجرا تصویری را باز می‌کند و چهار فیلتر توضیح داده شده را به ترتیب روی آن اعمال می‌کند.


تصویر ورودی


فیلتر جعبه‌ای نرمال شده با اندازه کرنل 25


فیلتر گوسی با اندازه کرنل 25


فیلتر میانه با اندازه کرنل 25


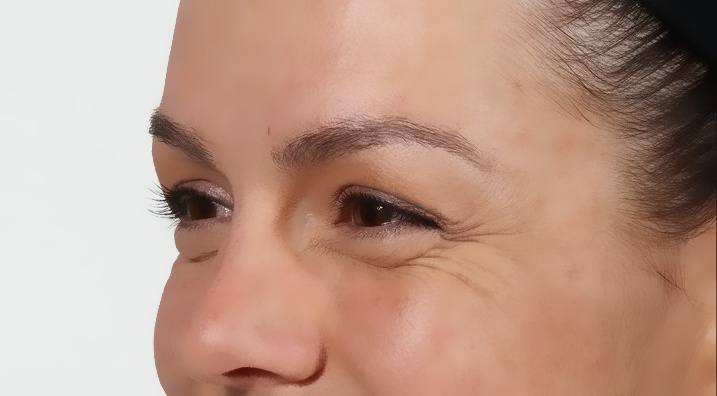
فیلتر دوگانه با اندازه کرنل 25

به راحتی می‌توان دید که کیفیت تصویر ایجاد شده با فیلتر دوگانه از سایر تصاویر بیشتر است.

Normalized Box Filter ↩
Gaussian Filter ↩
Median Filter ↩
Bilateral Filter ↩
Anchor Point ↩
Standard derivation ↩