فصل دوم - حوزهٔ مکان
تبدیل اَفاین
به هر تبدیلی که بتوان آن را به فرم یک ضرب ماتریسی و به دنبال آن یک جمع برداری بیان کرد، تبدیل اَفاین می گویند. بنابراین میتوانیم اعمال زیر را به عنوان تبدیل اَفاین در نظر بگیریم:
- چرخش (تبدیل خطی)
- انتقال (جمع برداری)
- عملیات مقیاسی (تبدیل خطی)
یک تبدیل اَفاین نشان دهندهٔ یک رابطه بین دو عکس است و معمولترین راه برای نشان دادن یک تبدیل اَفاین، استفاده از یک ماتریس 2 در 3 است:
با توجه به اینکه میخواهیم یک بردار دو بعدی به صورت $X = \begin{bmatrix} x \\ y \end{bmatrix}$ را با استفاده از A و B تبدیل کنیم، میتوانیم این کار را به صورت معادل زیر هم انجام دهیم:
گفتیم که هر تبدیل اَفاین یک رابطه بین دو عکس است. اطلاعات مربوط به این رابطه میتواند به دو طریق وجود داشته باشد:
- X و T را در اختیار داریم و می دانیم که این دو با هم رابطه دارند. بنابراین هدف ما پیدا کردن M است.
- M و X را در اختیار داریم و برای به دست آوردن T از معادله $T = M . X$ استفاده میکنیم. ممکن است M را به طور صریح در اختیارمان قرار دهند (یعنی همان ماتریس 2 در 3 را داده باشند)، یا اینکه آن را به صورت یک رابطهٔ هندسی بین نقاط داشته باشیم.
از آنجایی که M دو تصویر را به هم ربط میدهد، میتوان آن را به صورت سادهترین حالت یعنی حالتی که سه نقطه از هر کدام از دو تصویر را به هم ربط میدهد، در نظر گرفت. به شکل زیر نگاه کنید:
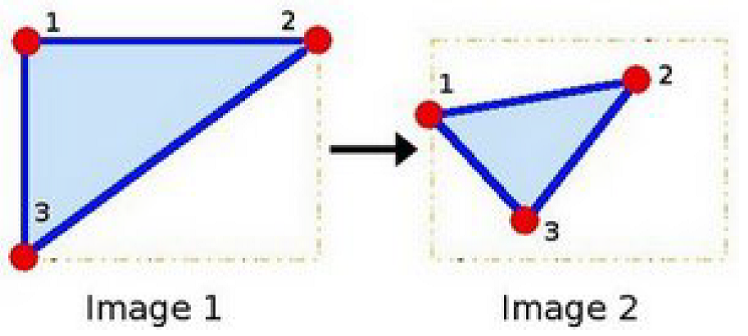
نقاط 1، 2 و 3 در تصویر 1 (که یک مثلث تشکیل دادهاند)، به تصویر 2 نگاشت شدهاند و هنوز هم به شکل یک مثلث هستند ولی شکل آن مثلث تغییر کرده است. اگر ما تبدیل اَفاین این سه نقطه را پیدا کنیم، میتوانیم آن را به همهٔ پیکسلهای یک تصویر اعمال کنیم.
کد
#include "opencv2/highgui/highgui.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include <iostream>
#include <stdio.h>
using namespace cv;
using namespace std;
/// Global variables
char* source_window = "Source image";
char* warp_window = "Warp";
char* warp_rotate_window = "Warp + Rotate";
/** @function main */
int main( int argc, char** argv )
{
Point2f srcTri[3];
Point2f dstTri[3];
Mat rot_mat( 2, 3, CV_32FC1 );
Mat warp_mat( 2, 3, CV_32FC1 );
Mat src, warp_dst, warp_rotate_dst;
/// Load the image
src = imread( argv[1], 1 );
/// Set the dst image the same type and size as src
warp_dst = Mat::zeros( src.rows, src.cols, src.type() );
/// Set your 3 points to calculate the Affine Transform
srcTri[0] = Point2f( 0,0 );
srcTri[1] = Point2f( src.cols - 1, 0 );
srcTri[2] = Point2f( 0, src.rows - 1 );
dstTri[0] = Point2f( src.cols*0.0, src.rows*0.33 );
dstTri[1] = Point2f( src.cols*0.85, src.rows*0.25 );
dstTri[2] = Point2f( src.cols*0.15, src.rows*0.7 );
/// Get the Affine Transform
warp_mat = getAffineTransform( srcTri, dstTri );
/// Apply the Affine Transform just found to the src image
warpAffine( src, warp_dst, warp_mat, warp_dst.size() );
/** Rotating the image after Warp */
/// Compute a rotation matrix with respect to the center of the image
Point center = Point( warp_dst.cols/2, warp_dst.rows/2 );
double angle = -50.0;
double scale = 0.6;
/// Get the rotation matrix with the specifications above
rot_mat = getRotationMatrix2D( center, angle, scale );
/// Rotate the warped image
warpAffine( warp_dst, warp_rotate_dst, rot_mat, warp_dst.size() );
/// Show what you got
namedWindow( source_window, CV_WINDOW_AUTOSIZE );
imshow( source_window, src );
namedWindow( warp_window, CV_WINDOW_AUTOSIZE );
imshow( warp_window, warp_dst );
namedWindow( warp_rotate_window, CV_WINDOW_AUTOSIZE );
imshow( warp_rotate_window, warp_rotate_dst );
/// Wait until user exits the program
waitKey(0);
return 0;
}
توضیح
همانطور که قبلاً توضیح داده شد، برای به دست آوردن یک تبدیل اَفاین به رابطهٔ بین دو مجموعه سه نقطهای نیاز داریم. در خطوط 30 تا 37 این دو مجموعه تعریف شدهاند. موقعیت این نقاط تقریباً شبیه همانی است که در قسمت قبل دیدید.
اکنون با داشتن این نقاط در خط 40 برای به دست آوردن تبدیل اَفاین از تابع getAffineTransform استفاده میکنیم. خروجی این تابع به صورت یک ماتریس 2 در 3 است.
در خط 43 با استفاده از تابع warpAffine تبدیل اَفاین را به تصویر src اعمال میکنیم. این تابع چهار آرگومان دارد:
- src: تصویر ورودی
- warp_dst: تصویر خروجی
- warp_mat: تبدیل اَفاین
- warp_dst.size(): اندازهٔ تصویر خروجی است.
در خطوط 48 تا 56 میخواهیم تصویر تبدیل شده warp_dst را بچرخانیم. برای چرخاندن یک تصویر به مختصات مرکزی که تصویر باید نسبت به آن بچرخد و میزان زاویهای که تصویر باید بچرخد نیاز داریم. این پارامترها در خطوط 48 تا 50 تعریف شدهاند.
در خط 53 برای تولید ماتریس چرخشی از تابع getRotationMatrix2D استفاده میکنیم. این تابع یک ماتریس 2 در 3 بر میگرداند.
سپس در خط 56، ماتریس چرخشی را به تصویر warp_mat اعمال میکنیم.
خروجی
 |
 |
|---|---|
| تصویر ورودی | تصویر تبدیل شده |
 |
|---|
| تصویر چرخیده شده از روی تصویر تبدیل شده |