فصل اول - معرفی
کلاس MAT
راههای متفاوتی برای بهدست آوردن عکسهای دیجیتال از دنیای بیرون وجود دارد: دوربینهای دیجیتال، اسکنرها، سی تی اسکن یا عکسبرداری رزونانس مغناطیسی، تنها چند مورد از این راهها هستند. در هر صورت چیزی که ما (انسانها) میبینیم، تنها یک عکس است. البته چیزی که دستگاههای دیجیتالِ ما ذخیره میکنند، تعدادی عدد به ازای هر نقطه در تصویر است.

مثلاً در تصویر بالا میبینید که آینهٔ خودرو تنها یک ماتریس عددی است؛ هر کدام از این عددها نمایانگر میزان روشنایی1 یک نقطهٔ عکس هستند. در نهایت همهٔ عکسهای موجود در یک کامپیوتر، تبدیل به ماتریسهای عددی به علاوهٔ اطلاعات شرح دهندهٔ آنها میشوند.
در ابتدای توزیع OpenCV، تنها از رابط C پشتیبانی میشد. در آن زمان برای ذخیرهٔ عکسها در حافظه از داده ساختار IplImage استفاده میشد. این روش تمام جنبههای بد زبان C را روی کار میآورد. اصلیترین مشکل، مدیریت دستیِ حافظه بود که برنامه نویس را مسئول اختصاص و باز پس گیری حافظه میکرد. البته ممکن است این موضوع در برنامههای کوچک خود نمایی نکند، ولی زمانی که برنامهها بزرگ و بزرگتر میشوند، دست و پنجه نرم کردن با این قضیه بسیار طاقت فرسا خواهد شد به گونهای که شما را از هدف اصلیتان دور میکند و به یک برنامه نویس سیستم مدیریت حافظه تبدیل میکند!
خوشبختانه با روی کار آمدن ++C و معرفی مفهوم شیءگرایی، راهی جدید به روی برنامه نویسان باز شد: مدیریت خودکار حافظه (البته کم و بیش). ++C کاملاً با C سازگار بوده و هیچ نگرانی در مورد برنامههای قدیمی وجود ندارد. بنابراین در نسخه دوم OpenCV، رابط جدید ++C با بهرهگیری از خواص شیءگرایی ++C ارائه شد که راهی جدید برای انجام کارها به برنامه نویس پیشنهاد میداد. راهی که برنامه نویس را کمتر درگیر مدیریت حافظه میکرد و کدها را شفافتر میساخت. قانونی نانوشته که میگفت «با کمتر نوشتن، چیزهای بیشتری به دست بیاور».
اولین چیزی که باید دربارهٔ Mat بدانید این است که دیگر نیازی به اختصاص دستی حافظه و آزاد کردن آن پس از اتمام کار ندارید. بیشتر تابعهای OpenCV دادههای خروجیشان را به صورت خودکار در مکانی از حافظه قرار میدهند (البته میتوان این کار را به صورت دستی هم انجام داد). میتوان یک شیء Mat ساخته شده را به تابعی ارسال کرد تا اگر اندازهٔ شیء ارسال شده فضای مورد نیاز را ارضا کرد، تابع از آن شیء برای ذخیرهٔ دادهها استفاده کند. با این ویژگی میتوانید در تمام برنامه تنها از اندازهای از حافظه استفاده کنید که برای انجام کارتان احتیاج دارید؛ نه بیشتر و نه کمتر.
Mat در واقع از دو قسمت تشکیل شده است:
- هدر که حاوی اطلاعاتی از قبیل اندازهٔ ماتریس، شیوهٔ ذخیره سازی، آدرس محل ذخیرهٔ ماتریس و... است.
- یک اشاره گر به ماتریسی که مقادیر پیکسلها در آن ذخیره شده است و بسته به شیوهٔ ذخیره سازی، ممکن است یک یا چند بعد داشته باشد.
اندازهٔ هدر برای همهٔ ماتریسها ثابت است ولی اندازهٔ ماتریس داده ممکن است از یک عکس تا عکس دیگر متفاوت باشد. بنابراین وقتی در قسمتی از برنامه میخواهید عکسی را کپی کنید، بیشترِ زمان صرف کپی کردن قسمت دادهایِ ماتریس میشود.
با وجود آنکه یک ماتریس داده میتواند بین چند شیء Mat مشترک باشد، زمانی که نیازی به آن نیست، آخرین شیئی که از آن استفاده کرده، آن را پاک خواهد کرد. بدین منظور از یک مکانیسم شمارش مرجع استفاده میشود. وقتی هدر یک شیء Mat کپی میشود، یک واحد به شمارنده درون ماتریس کپی شده اضافه شده و وقتی یک هدر پاک شود، این شمارنده کاهش مییابد؛ وقتی شمارنده به صفر رسید ماتریس آزاد میشود.
شیوه ذخیره سازی دادهها در کلاس Mat
از این کلاس میتوان برای ذخیره سازی یک ماتریس عددی n بعدی یک کاناله یا چند کاناله استفاده کرد. میتوانید عکسهای سیاه و سفید یا رنگی، بردارها و ماتریسهای عدد مختلط، نقاط، هیستوگرامها و... را در آن ذخیره کرد. چیدمان دادهها در ماتریس M به وسیلهٔ آرایهٔ M.step[] مشخص میشود؛ آدرس عناصر این ماتریس که به صورت $(i_{0},\ \ldots,i_{M.dims - 1})$ است ($0 \leq i_{k} < M.size\lbrack k\rbrack$)، از طریق فرمول زیر محاسبه می شود:
$$addr\left( M_{i_{0},\ldots,i_{M.dims - 1}} \right) = M.data + M.step\left\lbrack 0 \right\rbrack*i_{0} + M.step\left\lbrack 1 \right\rbrack*i_{1} + \ldots + M.step\left\lbrack M.dims - 1 \right\rbrack*i_{M.dims - 1}$$
برای آرایههای دو بعدی فرمول بالا به صورت زیر کاهش مییابد:
$$addr\left( M_{i,j} \right) = M.data + M.step\left\lbrack 0 \right\rbrack*i + M.step\left\lbrack 1 \right\rbrack*j$$
توجه کنید که رابطهٔ $M.step\left\lbrack i \right\rbrack \geq M.step\left\lbrack i + 1 \right\rbrack*M.size\lbrack i + 1\rbrack$ همواره برقرار است. این یعنی ماتریسهای دوبعدی به صورت سطر به سطر و ماتریسهای سه بعدی به صورت صفحه به صفحه و به همین صورت برای ماتریسهای با ابعاد بالاتر، شیوهٔ ذخیره سازی ادامه مییابد. $M.step\lbrack M.dims - 1\rbrack$ کوچکترین است و همواره برابر با M.elemSize() است.
ساخت شیء Mat
راههای خیلی زیادی برای ساخت یک شیء Mat وجود دارد. محبوبترین راهها به صورت زیر هستند:
سازندهٔ2 Mat:
cv::Mat M(2,2, CV_8UC3, cv::Scalar(0,0,255)); std::cout << "M = " << std::endl << " " << M << std::endl;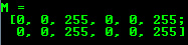
برای عکسهای دوبعدی و چند کاناله ابتدا تعداد ردیفها و ستونها را تعریف میکنیم. سپس نوع دادهای که برای ذخیرهٔ عناصر استفاده میکنیم و همچنین تعداد کانالهای ماتریس به ازای هر پیکسل را مشخص کرد. برای مشخص کردن نوع دادهها و تعداد کانالها میتوان از روش قراردادی زیر استفاده کرد:
CV_[تعداد بیتها برای هر آیتم][علامت دار یا بی علامت][پیشوند نوع]C[تعداد کانالها]مثلاً
CV_8UC3یعنی نوع داده 8 بیتی بی علامت سه کاناله است. این مقادیر برای حداکثر 4 کانال از پیش تعریف شدهاند. اگر به بیشتر از 4 کانال نیاز دارید، باید با استفاده از ماکرو زیر دادهٔ مورد نظر را تعریف کنید:CV_[تعداد بیتها برای هر آیتم][علامت دار یا بی علامت][پیشوند نوع]C(تعداد کانالها)مثلاً
CV_8UC(5)یک نوع 8 بیتی بدون علامت 5 کاناله درست میکند.Scalar هم یک بردار چهار عنصری است و با استفاده از آن میتوان در تمام پیکسلهای ماتریس تعریف شده، مقدار مشخصی را قرار داد.
استفاده از آرایه برای مشخص کردن ابعاد:
int sz[3] = {2,2,2}; cv::Mat L(3,sz, CV_8UC(1), cv::Scalar::all(0));مثال بالا طریقهٔ ساخت یک ماتریس با بیش از دو بعد را نشان میدهد. ابتدا با استفاده از یک آرایه ابعاد آن را مشخص میکنیم و سپس اشاره گر آن آرایه را به سازنده Mat ارسال میکنیم.
تابع
create():M.create(4,4, CV_8UC(2)); std::cout << "M = "<< std::endl << " " << M << std::endl;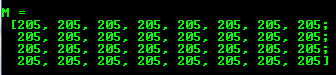
در این روش نمیتوان ماتریس را مقدار دهی اولیه کرد. این تابع فقط در صورتی که ماتریس قدیمی به اندازهٔ کافی فضا برای ماتریس جدید نداشته باشد، آن را مجدداً مقدار دهی میکند.
شیوه MATLAB: با استفاده از توابع
zeros()،ones()وeyes()میتوان مطابق با روش متلب، ماتریسهای مختلفی ساخت:cv::Mat E = cv::Mat::eye(4, 4, CV_64F); std::cout << "E = " << std::endl << " " << E << std::endl; cv::Mat O = cv::Mat::ones(2, 2, CV_32F); std::cout << "O = " << std::endl << " " << O << std::endl; cv::Mat Z = cv::Mat::zeros(3,3, CV_8UC1); std::cout << "Z = " << std::endl << " " << Z << std::endl;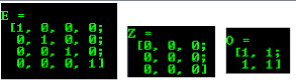
برای ماتریسهای کوچک میتوان از روش زیر استفاده کرد:
cv::Mat C = (cv::Mat_<double>(3,3) << 0, -1, 0, -1, 5, -1, 0, -1, 0); std::cout << "C = " << std::endl << " " << C << std::endl;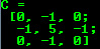
در اینجا Mat_ یک کلاس الگو برای Mat است که در بخشهای بعد به طور مفصل توضیح داده شده است.
clone کردن یا copyTo کردن قسمتی از یک ماتریس:
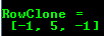
cv::Mat RowClone = C.row(1).clone(); std::cout << "RowClone = " << std::endl << " " << RowClone;در این روش تمام ماتریس (یعنی هم هدر و ماتریس داده) کپی میشوند.
دسترسی به عناصر درون شیء Mat
برای دسترسی به عناصر درون یک شیء Mat چهار راه وجود دارد که در زیر هر یک را به صورت جداگانه بررسی میکنیم.
برای نشان دادن این روشها و همچنین مقایسه آنها با هم یک کاربرد واحد را در نظر میگیریم. هدف این کاربرد جایگزینی مقادیر یک ماتریس بر اساس یک جدول است.
روش بهینه
وقتی بحث کارایی پیش میآید، نمیتوان در مقابل شیوهٔ قدیمی زبان C برای دسترسی به عناصر حافظه، یعنی عملگر [] (اشارهگر) ایستاد. بنابراین بهینهترین روشی که میتوان پیشنهاد کرد روش زیر است:
cv::Mat& ScanImageAndReduceC(cv::Mat& I, const uchar* const table)
{
// accept only char type matrices
CV_Assert(I.depth() != sizeof(uchar));
int channels = I.channels();
int nRows = I.rows;
int nCols = I.cols * channels;
if (I.isContinuous())
{
nCols *= nRows;
nRows = 1;
}
int i,j;
uchar* p;
for( i = 0; i < nRows; ++i)
{
p = I.ptr<uchar>(i);
for ( j = 0; j < nCols; ++j)
{
p[j] = table[p[j]];
}
}
return I;
}
در اینجا به صورت ساده فقط یک اشاره گر به ابتدای هر سطر به دست آورده و سپس آن را تا انتها ادامه میدهیم. در حالت خاصی که ماتریس تنها در یک سطر ذخیره شده، کافی است تنها یک بار اشاره گر سطر را درخواست کنیم و سپس تا انتهای آن رفته تا به تمام پیکسلهای ماتریس دسترسی داشته باشیم. باید مراقب عکسهای رنگی بود؛ از آنجایی که در این عکسها سه کانال داریم، پس لازم است روی سه برابر آیتمِ بیشتر در هر سطر حرکت کنیم.
راه دیگری هم برای این کار وجود دارد. متغیر data در شیء Mat، اشاره گری به اولین سطر و ستون است. اگر این اشاره گر پوچ باشد، دادهٔ معتبری در آن شیء وجود نخواهد داشت. بررسی کردن این اشاره گر سادهترین راه برای مطمئن شدن از بارگذاری صحیح عکس است. در حالتی که ذخیره سازی به صورت پشت سر هم باشد، میتوان از این روش برای دسترسی به پیکسلها استفاده کرد. در مورد عکس سیاه و سفید به صورت زیر عمل میکنیم:
uchar* p = I.data;
for( unsigned int i =0; i < ncol*nrows; ++i)
*p++ = table[*p];
نتیجه این کد مطابق با نتیجهٔ کد قبل است با این تفاوت که در اینجا با کدی پیچیدهتر روبرو هستیم که خوانایی کمتری هم دارد. جالب است بدانید که این کد در اجرا عملکرد مشابه ای با کد قبل دارد.
روش امن
در روش بهینه برنامه نویس باید مراقب حفرههای احتمالی بین سطرها باشد و تعداد فیلدهای مورد بررسی را کنترل کند (تا بیشتر یا کمتر از مقدار موجود نشود). روش امن از آن جهت که این نگرانیها را ندارد، روش امنتری است. تنها کاری که باید انجام داد این است که iterator شروع و پایان ماتریس را درخواست کرده و سپس فقط iterator شروع را افزایش داده تا به iterator پایان برسد. برای به دست آوردن مقدار اشاره شده توسط iterator، از عملگر * استفاده میکنیم (قبل از آن قرار میدهیم).
cv::Mat& ScanImageAndReduceIterator(cv::Mat& I, const uchar* const table)
{
// accept only char type matrices
CV_Assert(I.depth() != sizeof(uchar));
const int channels = I.channels();
switch(channels)
{
case 1:
{
cv::MatIterator_<uchar> it, end;
for( it = I.begin<uchar>(), end = I.end<uchar>(); it != end; ++it)
*it = table[*it];
break;
}
case 3:
{
cv::MatIterator_<Vec3b> it, end;
for( it = I.begin<Vec3b>(), end = I.end<Vec3b>(); it != end; ++it)
{
(*it)[0] = table[(*it)[0]];
(*it)[1] = table[(*it)[1]];
(*it)[2] = table[(*it)[2]];
}
}
}
return I;
}
در عکسهای رنگی سه آیتم uchar در هر ستون وجود دارد و میتوان آنها را به صورت یک بردار کوچک از آیتمهای uchar در نظر گرفت که در OpenCV با نام Vec3b شناخته میشوند. بنابراین اگر از یک iterator نوع uchar استفاده کنید، تنها به مقادیر کانال آبی دسترسی خواهید داشت. برای دسترسی به nامین زیر ستون از عملگر سادهٔ [] استفاده میکنیم. به خاطر بسپارید که iterator های OpenCV روی ستونها حرکت میکنند و به صورت خودکار به سطر بعدی میروند.
روش بیدرنگ
استفاده از این روش برای مرور تصاویر پیشنهاد نمیشود. از این روش باید زمانی که تعداد دسترسیهایمان کم است استفاده کرد. برای استفاده از روش بیدرنگ، باید سطر و ستون پیکسل مورد نظر و نوع داده را مشخص کنیم. برای عکسهای سیاه و سفید به صورت زیر عمل میکنیم:
cv::Mat& ScanImageAndReduceRandomAccess(cv::Mat& I, const uchar* const table)
{
// accept only char type matrices
CV_Assert(I.depth() != sizeof(uchar));
const int channels = I.channels();
switch(channels)
{
case 1:
{
for( int i = 0; i < I.rows; ++i)
for( int j = 0; j < I.cols; ++j )
I.at<uchar>(i,j) = table[I.at<uchar>(i,j)];
break;
}
case 3:
{
cv::Mat_<Vec3b> _I = I;
for( int i = 0; i < I.rows; ++i)
for( int j = 0; j < I.cols; ++j )
{
_I(i,j)[0] = table[_I(i,j)[0]];
_I(i,j)[1] = table[_I(i,j)[1]];
_I(i,j)[2] = table[_I(i,j)[2]];
}
I = _I;
break;
}
}
return I;
}
تابع at() نوع داده را به صورت الگو از ورودی میگیرد و آدرس آیتم درخواست شده را به صورت بیدرنگ محاسبه میکند و سپس یک اشاره گر به آن بر میگرداند.
در خط 4 بررسی میکنیم که ماتریس I از نوع کاراکتری باشد (یعنی یک بایتی باشد).
اگر میخواهید به صورت مکرر به منظور دسترسی به پیکسلهای یک عکس از این روش استفاده کنید، نوشتن نوع داده و کلید واژهٔ at برای هر دسترسی میتواند دردسر ساز و وقت گیر باشد. برای حل این مشکل، OpenCV یک نوع داده به نام Mat_ ارائه میدهد که کاملاً مشابه Mat است و فقط باید هنگام تعریف آن، نوع داده را مشخص کرد. در این داده ساختار میتوان از عملگر () برای دسترسی سریع به عناصر ماتریس استفاده کرد. همچنین میتوانید داده ساختارهای Mat و Mat_ را به راحتی به هم تبدیل کنید. در خط 17 کد بالا مشاهده میکنید که ابتدا ماتریس I را به یک شیء از نوع Mat_ با نوع داده Vec3b تبدیل میکنیم، سپس در خطوط 21 تا 23 با استفاده از عملگر () به دادههای هر عنصر ماترسی دسترسی پیدا میکنیم. به هر حال سرعت این روش در مقایسه با روش اول (یعنی استفاده از تابع at()) هیچ فرقی نمیکند.
روش جدول جستجو
در این روش از جدولِ جستجو برای تغیر مقدار پیکسلهای یک عکس استفاده میکنیم. جایگزین کردن مقدار پیکسلهای یک عکس با مقدارهای جدید یک کار معمول در پردازش تصویر است. به همین خاطر OpenCV تابعی ارائه داده که این کار را به صورت خودکار برای ما انجام میدهد و دیگر نیازی نیست که خودمان روی همهٔ پیکسلهای تصویر حرکت کنیم و مقدار پیکسلها را با مقدارهای جدید جایگزین کنیم. این تابع LUT() است. برای شروع باید یک جدول جستجو بسازیم. برای این کار از یک شیء Mat استفاده میکنیم:
cv::Mat lookUpTable(1, 256, CV_8U);
uchar* p = lookUpTable.data;
for( int i = 0; i < 256; ++i)
p[i] = table[i];
سپس تابع LUT را روی عکس ورودی صدا میزنیم (I عکس ورودی و J هم عکس خروجی است):
cv::LUT(I, lookUpTable, J);
مقایسه روشها
برای اینکه بهتر بتوان تفاوت کارایی را دید، از یک عکس رنگی بسیار بزرگ ($2560\times1600$ پیکسلی) استفاده شده و به منظور حصول دقت بیشتر، از زمانهای به دست آمده در 100 بار اجرای متوالی برای هر روش، میانگین گرفته شده است.
| روش | زمان اجرا (میلی ثانیه) |
|---|---|
| بهینه | 79.4717 |
| امن | 83.7201 |
| بیدرنگ | 93.7878 |
| جدول جستوجو | 32.5759 |
از این جدول چند نتیجه میتوان گرفت:
- تا حد امکان از تابعهایی که OpenCV ارائه داده است استفاده کنید زیرا کتابخانهٔ OpenCV از چند نخی پشتیبانی میکند.
- روش امن با وجود اینکه امنترین روش است اما بسیار کند عمل میکند.
- پرهزینهترین روش، روش بیدرنگ است. البته این در حالت اجرای خطایابی است و ممکن است در حالت انتشار بهتر از روش امن عمل کند ولی مطمئناً در زمینهٔ امنیت از روش امن عقبتر است.
عملگرهای ریاضی
در لیست زیر عملگرهای ریاضی پشتیبانی شده توسط کلاس Mat را میبینید. میتوانید هر کدام از این عملگرها را برای ایجاد عبارتهای پیچیده با هم ترکیب کرد. در اینجا A و B ماتریسهایی از نوع Mat هستند و s یک نوع Scalar است و alpha هم یک مقدار حقیقی اسکالر است.
جمع، تفریق و نقیض: $A + B,\ A - B,\ A + s,\ A - s,\ s + A,\ s - A,\ - A$
مقیاس گذاری3: $A*alpha$
ضرب و تقسیم درایهای: $A.mul\left( B \right),\ A/B,\ alpha/A$
ضرب ماتریسی: $A*B$
ترانهاده: $A.t()$
معکوس و شبه معکوس ماتریس، حل سیستمهای خطی و مسائل کمترین مربعات:
$$A.inv\left( \left\lbrack \text{method} \right\rbrack \right)\ \left( \sim\ A^{- 1} \right)\ ,\ A.inv\left( \left\lbrack \text{method} \right\rbrack \right)*B\ (\sim\ X:AX = B)$$
مقایسه: عبارتهای $A\ comop\ B,\ A\ comop\ alpha,\ alpha\ comop\ A$ که $comop$ میتواند یکی از عملگرهای =<، =>، >، <، == یا =! باشد. نتیجهٔ مقایسه یک ماسک یک کاناله 8 بیتی است که عناصر آن در صورت بر قرار بودن شرایط مقدار 255 و در صورت برقرار نبودن مقدار صفر دارند.
عملگرهای بیتی: عبارتهای $A\ logicop\ B,\ A\ logicop\ s,\ s\ logicop\ A,\ \sim A$ که $logicop$ میتواند یکی از عملگرهای $\&,\ |,\ \hat{}$ باشد.
کمینه و بیشینه درایهای: $\min\left( A,\ B \right),\max\left( A,\ B \right),\min\left( A,\ alpha \right),\ max(A,\ alpha)$
قدر مطلق درایهای: $abs(A)$
ضرب داخلی4 و خارجی5: $\text{A.cross}\left( B \right),\ A.dot(B)$
توابعی مثل norm، mean، sum، countNonZero، trace، determinant، repeat و... که یک ماتریس یا یک مقدار اسکالار بر میگردانند.
مقدار دهندههای ماتریس (مثل
Mat::eye()وMat::zeros()وMat::ones())، مقدار دهندههای به وسیلهٔ کاما، سازندههای ماتریس و عملگرهای که یک زیر ماتریس را استخراج میکنند.سازندههای به شکل
Mat_<destination_type>()که ماتریس را به نوع مناسب تبدیل میکنند.